遗传算法,核心是达尔文 优胜劣汰适者生存的进化理论的思想。 我们都知道一个种群,通过长时间的繁衍,种群的基因会向着更适应环境的趋势进化,牛B个体的基因被保留,后代越来越多,适应能力低个体的基因被淘汰,后代越来越少。经过几代的繁衍进化,留下来的少数个体,就是相对能力最强的个体了。 那么在解决一些问题的时候,我们能不能学习这样的思想,比如先随机创造很多很多的解,然后找一个靠谱的评价体系,去筛选比较好的解 ,再用这些好的解像生小宝宝一样生一堆可能更好的解,然后再筛再生,反复弄个几代,得到的说不定就是近似最优解哟 说干就干,有一个经典组合问题叫“背包问题”,我们拿这种思路来试试 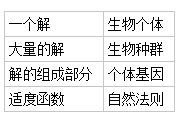 这样参照着我们熟悉的知识体系,去理解学习,原来听上去遥不可及的理论是不是一下就变得亲切易懂了吧? 可是我们再看一些教科书或者就拿百度百科来说(怕也是摘抄的某本书上的段落) <img src="https://pic3.zhimg.com/fa57bc9d938dece834eb7d4f31cf856a_b.jpg" data-rawwidth="804" data-rawheight="236" class="origin_image zh-lightbox-thumb" width="804" data-original="https://pic3.zhimg.com/fa57bc9d938dece834eb7d4f31cf856a_r.jpg">真的是通篇不说人话啊!对已经了解这个算法思想的人来说,还能勉强硬着头皮看下去,但对入门者来说,这TMD简直就是噩梦!而这完全是国内各种教材的通病!
这样参照着我们熟悉的知识体系,去理解学习,原来听上去遥不可及的理论是不是一下就变得亲切易懂了吧? 可是我们再看一些教科书或者就拿百度百科来说(怕也是摘抄的某本书上的段落) <img src="https://pic3.zhimg.com/fa57bc9d938dece834eb7d4f31cf856a_b.jpg" data-rawwidth="804" data-rawheight="236" class="origin_image zh-lightbox-thumb" width="804" data-original="https://pic3.zhimg.com/fa57bc9d938dece834eb7d4f31cf856a_r.jpg">真的是通篇不说人话啊!对已经了解这个算法思想的人来说,还能勉强硬着头皮看下去,但对入门者来说,这TMD简直就是噩梦!而这完全是国内各种教材的通病!  真的是通篇不说人话啊!对已经了解这个算法思想的人来说,还能勉强硬着头皮看下去,但对入门者来说,这TMD简直就是噩梦!而这完全是国内各种教材的通病! 我其实一直在想,教材面向的明明就是望门欲入的初学者,你不弄得生动活泼一点招徕门徒就算了,在一群幼儿园小朋友面前卖弄之乎者也还显本事了是么!我是还记得我们学校的高数书编的有多么生涩难懂,结果第一节课老教授上课时还说“我们不用同济的版本,那本书太浅,不适合我们学校的学生” 可是在我和大多数同学看来,同济版本的高数倒更像是为了要入门的同学编写的教材,自己学校编的那本却更像是给同行评阅炫耀作者深度的大部头。 知识明明可以讲的更有趣,让人愿意入其门来探个究竟。
真的是通篇不说人话啊!对已经了解这个算法思想的人来说,还能勉强硬着头皮看下去,但对入门者来说,这TMD简直就是噩梦!而这完全是国内各种教材的通病! 我其实一直在想,教材面向的明明就是望门欲入的初学者,你不弄得生动活泼一点招徕门徒就算了,在一群幼儿园小朋友面前卖弄之乎者也还显本事了是么!我是还记得我们学校的高数书编的有多么生涩难懂,结果第一节课老教授上课时还说“我们不用同济的版本,那本书太浅,不适合我们学校的学生” 可是在我和大多数同学看来,同济版本的高数倒更像是为了要入门的同学编写的教材,自己学校编的那本却更像是给同行评阅炫耀作者深度的大部头。 知识明明可以讲的更有趣,让人愿意入其门来探个究竟。
作者:弹弹弹球 链接:https://www.zhihu.com/question/23293449/answer/29287544 来源:知乎 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。 “背包问题(Knapsack problem)是一种 的 问题。问题可以描述为:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。”这个问题的衍生简化问题 “0-1背包问题” 增加了限制条件:每件物品只有一件,可以选择放或者不放,更适合我们来举例 这样的问题如果数量少,当然最好选择穷举法 比如一共3件商品,用0表示不取,1表示取,那么就一共有 000 001 010 011 100 101 110 111 这样8种方案,然后让计算机去累加和,与重量上限比较,留下来的解里取最大即可。 但如果商品数有300,3000,甚至3w种呢,计算量太大穷举法可能就不适用了,这时如果遗传算法使用得当,就能在较短的时间内帮我们找到近似的最优解,我们继续往下看: 新的问题是12件商品的0-1背包问题 我们先让计算机随机产生1000个12位的二级制数 把总重量超过背包上限的解筛掉 剩下的两两一对随机交换“基因片段”产生下一代 交换前: 0000 1100 1101 0011 0101 0101 交换后: 0000 0101 1101 0011 1100 0101 再筛选,再交配,如此反复几代,留下的解携带的“基因“差不多就是最好的了,怎么样跟生物进化是不是一模一样? 其实还差点,生物繁殖过程中,新产生的基因是有一定几率突变的,这是很多优良性状的重要来源,遗传算法中可也不能忽略它
比如:
变异前:
000101100101
变异后:
000101110101
那也有人得疑惑了,我怎么知道要让哪个地方产生突变呢?其实蜘蛛侠NB之前,他也不知道蜘蛛咬在那能让他变NB而不是SB,这就是一个概率问题。我们在设计算法的时候,会给每个基因设置一个突变概率(当然是非常非常小了)同样的在基因交换阶段交换哪些基因呢,也是一个算法设置问题。 总结一下,遗传算法应该有 一个基本函数:适度函数f(x) 三个基本操作:选择,交叉,变异 一.适度函数 适度函数很好理解,其实就是指解的筛选标准,比如我刚才说的把所有超过上限重量的解筛选掉,但是不是有更好的筛选标准或者这个现有的标准根本就是个渣呢?这将直接影响最后结果的接近程度以及求解所耗费的时间,所以设置一个好的适度函数很重要 二.选择 刚才为了大家理解方便,我直接让所有解都参与了后续的交叉以及变异,但真实世界可不是这样子的,因为也不是每个人都会结婚生子的对吧。 说直白点,所谓【屌丝注孤生】【工科男注孤生】什么的还不是因为loser的基因不适合往下传呗。不过实际情况是我们偶尔也能看到或听到屌丝逆袭、鲜花牛粪之类励志故事,只不过频率比较低咯 没错,概率!在遗传算法中 选择也是个概率问题,在解的世界中(姑且这么称呼吧)适度更高的高富帅们是不是应该有更高的概率被选去传宗接代才合适呢?不过和现实世界一样,适度低的屌丝解是要给人家一点希望的对不对?所以 在选择一些解来产生下一代时,一种常用的选择策略是 “比例选择”,也就是个体被选中的概率与其适应度函数值成正比。假设群体的个体总数是M,那么那么一个体Xi被选中的概率为f(Xi)/( f(X1) + f(X2) + …….. + f(Xn) ) 三.交叉 这是例子中详细说到的,交换两个解的部分”基因”,来构造两个子代的解。 四.变异 在繁殖子代的过程中,新产生的解中的“基因”会以一定的概率出错,称为变异。我们可以吧变异发生的概率设置为Pm 五.基本遗传算法优化 精英主义:这是基本遗传算法的一种优化。目的是防止进化过程中产生的最优解被变异和交叉所破坏。《遗传算法原理及应用》介绍的最优保存策略是:即当前种群中适应度最高的个体不参与交叉运算和变异运算,而是用它来替换掉本代群体中经过交叉、变异等遗传操作后所产生的适应度最低的个体。 后记: 其实不管是遗传算法,还是模拟退火算法或者其他算法,其本质都是借鉴自然界中的规则规律,人为的为问题设置了一个模拟模型,然后用大自然告诉我们的规律去找最优解,在理解这些算法的时候,可以照着这个思路去走,一般能让你快速拨云见日,了解算法的核心思想。 比如遗传算法,我们可以对比种群的进化,给问题设置的模型就是: <img src="https://pic2.zhimg.com/013cfe6389cf204b226616d5194270b1_b.jpg" data-rawwidth="181" data-rawheight="117" class="content_image" width="181">这样参照着我们熟悉的知识体系,去理解学习,原来听上去遥不可及的理论是不是一下就变得亲切易懂了吧? 这样参照着我们熟悉的知识体系,去理解学习,原来听上去遥不可及的理论是不是一下就变得亲切易懂了吧? 可是我们再看一些教科书或者就拿百度百科来说(怕也是摘抄的某本书上的段落) <img src="https://pic3.zhimg.com/fa57bc9d938dece834eb7d4f31cf856a_b.jpg" data-rawwidth="804" data-rawheight="236" class="origin_image zh-lightbox-thumb" width="804" data-original="https://pic3.zhimg.com/fa57bc9d938dece834eb7d4f31cf856a_r.jpg">真的是通篇不说人话啊!对已经了解这个算法思想的人来说,还能勉强硬着头皮看下去,但对入门者来说,这TMD简直就是噩梦!而这完全是国内各种教材的通病!
这样参照着我们熟悉的知识体系,去理解学习,原来听上去遥不可及的理论是不是一下就变得亲切易懂了吧? 可是我们再看一些教科书或者就拿百度百科来说(怕也是摘抄的某本书上的段落) <img src="https://pic3.zhimg.com/fa57bc9d938dece834eb7d4f31cf856a_b.jpg" data-rawwidth="804" data-rawheight="236" class="origin_image zh-lightbox-thumb" width="804" data-original="https://pic3.zhimg.com/fa57bc9d938dece834eb7d4f31cf856a_r.jpg">真的是通篇不说人话啊!对已经了解这个算法思想的人来说,还能勉强硬着头皮看下去,但对入门者来说,这TMD简直就是噩梦!而这完全是国内各种教材的通病!  真的是通篇不说人话啊!对已经了解这个算法思想的人来说,还能勉强硬着头皮看下去,但对入门者来说,这TMD简直就是噩梦!而这完全是国内各种教材的通病! 我其实一直在想,教材面向的明明就是望门欲入的初学者,你不弄得生动活泼一点招徕门徒就算了,在一群幼儿园小朋友面前卖弄之乎者也还显本事了是么!我是还记得我们学校的高数书编的有多么生涩难懂,结果第一节课老教授上课时还说“我们不用同济的版本,那本书太浅,不适合我们学校的学生” 可是在我和大多数同学看来,同济版本的高数倒更像是为了要入门的同学编写的教材,自己学校编的那本却更像是给同行评阅炫耀作者深度的大部头。 知识明明可以讲的更有趣,让人愿意入其门来探个究竟。
真的是通篇不说人话啊!对已经了解这个算法思想的人来说,还能勉强硬着头皮看下去,但对入门者来说,这TMD简直就是噩梦!而这完全是国内各种教材的通病! 我其实一直在想,教材面向的明明就是望门欲入的初学者,你不弄得生动活泼一点招徕门徒就算了,在一群幼儿园小朋友面前卖弄之乎者也还显本事了是么!我是还记得我们学校的高数书编的有多么生涩难懂,结果第一节课老教授上课时还说“我们不用同济的版本,那本书太浅,不适合我们学校的学生” 可是在我和大多数同学看来,同济版本的高数倒更像是为了要入门的同学编写的教材,自己学校编的那本却更像是给同行评阅炫耀作者深度的大部头。 知识明明可以讲的更有趣,让人愿意入其门来探个究竟。